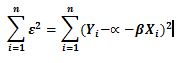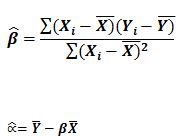
REGRESYON ANALİZİ
Regresyon analizi, aralarında sebep-sonuç ilişkisi bulunan iki veya daha fazla değişken arasındaki ilişkiyi belirlemek ve bu ilişkiyi kullanarak o konu ile ilgili tahminler ya da kestirimler yapabilmek amacıyla yapılır.
Örnek: Sebep Sonuç
- Gelir Harcama
- Çalışma süresi Alınan not
- Faiz Tasarruf
Bu analiz tekniğinde iki (basit regresyon) veya daha fazla değişken (çoklu regresyon) Arasındaki ilişki açıklamak için matematiksel bir model kullanılır ve bu model regresyon modeli olarak adlandırılır.
1.Basit regresyon modeli
Y=α+βX+ε Şeklinde bir bağımlı ve bir de bağımsız değişken içeren bir modeldir.
Bu modelde;
Y; bağımlı (sonuç) değişken olup belli bir hataya sahip olduğu varsayılır.
X; bağımsız (sebep) değişkeni olup hatasız ölçüldüğü varsayılır.
α; sabit olup X=0 olduğunda Y’nin aldığı değerdir.
Β; regresyon katsayısı olup, X’in kendi birimi cinsinden 1 birim değişmesine karşılık Y’de
kendi birimi cinsinden meydana gelecek değişme miktarını ifade eder.
ε; tesadüfi hata terimi olup ortalaması sıfır varyansı σ2 olan normal dağılış gösterdiği varsayılır. Bu varsayım parametre tahminleri için değil katsayıların önem kontrolleri için gereklidir.
2.Parametrelerin (Katsayıların) Tahmini;
Bir regresyon modeli oluşturulurken genelde en-küçük kareler ve en büyükolabilirlik teknikleri olarak bilinen iki yaklaşımdan birisi kullanılır. Eğer hata teriminin normal dağılım göstermesi seklinde bir varsayım varsa en büyük olabilirlik, hata teriminin dağılışı ile ilgili herhangi bir varsayım söz konusu değilse en-küçük kareler tekniği kullanılarak parametreler tahmin edilir.
3.En-Küçük Kareler yönteminde parametre tahmini;
Alman matematikçi Carl Friedrich Gauss’a ait olan en küçük kareler yöntemi cazip istatistiki özelliklerinden dolayı regresyon analizi için kullanılan en popüler yöntemlerden biridir.
Kurulan regresyon modeli ilgilenilen problemle ilgili örnek olarak alınmış gözlem değerleri kullanılarak hesaplanmaya çalışılır. Bu nedenle kurduğumuz modeldeki değerler tahmini değerler olacaktır.
Tahmin edilen katsayıların ve değişkenlerin hesaplanması için geliştirilen ve gerçek katsayılara en yakın sonuçları elde edebilmek için EKK yöntemiyle gerçek Y değerleri ile tahmin edilen Y değerleri arasındaki farkın kareleri toplamını minimum yapılır.
Matematiksel olarak amacımız Y=α+βX+ε denklemindeki ε (hata teriminin) en küçük değer almasını sağlamaktır.
ε =α+βX -Y
Hata teriminin tüm gözlemler için kareleri alınır ve toplanırsa (Hata Kareleri Toplamı –HKT)
En-Küçük Kareler tekniğinde HKT’nı en küçük yapabilmek için yukarıdaki ifadenin α ve β ya göre türevleri alınıp sıfıra eşitlenerek Normal denklemler diye adlandırdığımız denklem sistemi elde edilir.
NORMAL DENKLEMLER
Buradan α ve β çekilirse
Açıklayıcı Örnek
Kardiyoloji kliniğine başvuran erkek hastalar üzerinde yapılan bir araştırmada, yas(x) ve kolesterol(y) değişkeni arasındaki korelasyondan yola çıkılarak kurulan regresyon modeli aşağıdaki gibi elde edilmiştir:
Y=3,42+0,326x
Bu modele göre, yastaki bir birimlik artısın, kolesterol değerinde 0.326 birimlik bir artışa neden olacağı, yeni doğan bir erkeğin (X=0) kolesterol değerinin ise 3.42 olacağı söylenebilir. Kurulan bu modele göre, 50 yasında bir erkeğin kolesterol değerinin ne kadar olacağını tahmin edebiliriz.
X=50 için :
Y=3,42+0,326*(50)=19,52
50 yasında bir erkeğin kolesterol değerinin 19.52 olacağı söylenebilir.